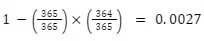The Birthday Problem - Amazing Mathematical Fact Explained
What number of people need to gather in a room before there is a 50 percent chance of at least two people sharing a date of birth?
To most people, intuition says the answer to the question is 183, half the days of the year. That allows for a 50/50 chance of finding people with matching birthdays. Other guess numbers way higher, most often more than 365.
In a surprising twist, the correct answer is quite small. So small it might shock you. Let’s delve into the birthday problem - what it is, how to solve it, and why it is a paradox.
What is the Birthday Problem?
The birthday problem is also sometimes referred to as the birthday paradox, probability theory, and birthday surprise. The crux of it is that in a room of 23 people, there is a 50 percent chance of two people sharing the same birthday.
Sounds fake, right? The probability of finding two people that share a birthday in such a small pool seems highly unlikely.
How is it possible that out of 23 people in a room, there is a 50 percent chance that at least one pair have a shared birthday when there are 365 days in a year?
Most of us, subconsciously, only think about finding somebody with a similar birthday to us. If there are only 22 other people, there will only be 22 other probable birthdays. It would feel more like luck than any statistical probability.
Instead, the birthday problem is comparing all birthday matches, not just ours. So while there might not be someone who shares the same birthday as you in a room of 23 people, chances are two other people in the room do. Probably people that were born in September, the month with the most births.
How Do You Solve the Birthday Paradox?
The mathematics involved with the birthday paradox disregards leap years and twins. While more people are born at a certain time of the year, for this, we’ll take for granted that all birthdays have an equal probability of occurring.
Let’s enter a room and imagine there is one person. This person only has one birthday (of course), which means there is a 365/365 chance that there is not a shared birthday in the room with this person.
Let’s add another person to the room. The first person already covers one possible birthday. This means the new person has a 364/365 chance of not sharing the same birthday.
Multiply these probabilities and subtract them from one.
That leaves us with a 0.0027 chance of having a match. Not great odds.
Add a third person to the room and repeat the equation. Multiply the probabilities and subtract them from one.
That leaves us with a 0.0082 chance of a match.
As you can see, a pattern is slowly emerging. But it still feels like it would take a whole lot of people to reach a 50 percent chance of meeting two people who share a birth date.
Surprisingly, when the equation carries on, the probability rises really fast. With only five people together, there is already a 2.7 percent chance of at least one match. With ten people, it rises to an 11.7 percent chance.
By 23, there is a 50.7 percent chance of at least one birthday. If there were 70 people together, having a match is virtually guaranteed.
Isn’t 23 Too Little?
We’re all a little selfish and subconsciously only think of our own birthdays. In a group of 23, we’ve assumed there are only 22 birthdays to act as comparisons. But when comparing all different birthdays, not just our own, there are 253 comparisons that can be made. That’s more than half the days of the year.
How does this work?
Well, the first person compares their birthday to 22 distinct birthdays. If we assume the person’s birthday didn’t have a birthday match, the next person can step up and compare their birthday.
Because the first one didn’t share the same birthday with anyone, they are taken out of the pool of probable matches. The second person then compares their birthday to the 21 other people.
If the second birthday didn’t match, the third person could compare their birthday with the 20 others. It carries on and on (22 + 21 + 20 etc.). The sum of these leaves us with 253 combinations in a room of 23 people.
We mentioned before that this equation doesn’t account for leap years and assumes all birthdays have an equal likelihood of occurring. Adding these back into the equation will likely change it completely, right? Wrong.
Adding these into the equations didn’t change much at all. It just further proved the birthday problem. As an add-on, it was proven that in a group of 88 people, it’s likely that three random people share the same birth date.
Why Is It A Paradox?
This concept isn’t really a paradox. The only reason most consider it a paradox is because people find it a little ridiculous that it only takes 23 to find one pair that share a birthday.
We tend only to consider scenarios in relation to ourselves, and this paradox takes us out of it. Our birthday, our special day, isn’t really ours.
Who Invented The Birthday Paradox?
So, who noticed this ‘paradox’ in the first place?
The birthday paradox is generally unofficially credited to Harold Davenport in 1927. Strangely, he never published anything and never claimed to have discovered the matter because he “could not believe it had not been stated before.”
The official credit instead went to Richard von Mises in 1939, when he published a version of the birthday problem.
Conclusion
The birthday problem throws intuition out the window and makes a lot of people uncomfortable about how common their date of birth is. It’s been proven true multiple times and can easily be verified with a control group. And yet, it still feels so completely out there for most.
Instead of getting hung up on your birthday not being yours alone, think about how cool it is that your special day is also one for many other people to share!
For other simple explanations of complex scientific facts, check out our articles on Phreeque.com.